Complex Systems and Dynamics

Complex systems are omnipresent in everyday life, and their highly dynamic nature makes dealing with them a challenging task.

About the research group

Mathematical modeling transforms the investigation of complex systems into an investigation of the corresponding models, in which mathematical tools are used to describe, explain, analyze or predict the dynamics.

In our research group, we aim at developing systematic approaches to investigate the dynamics of systems arising from natural, social, and life sciences.

Research topics include (but not limited to):

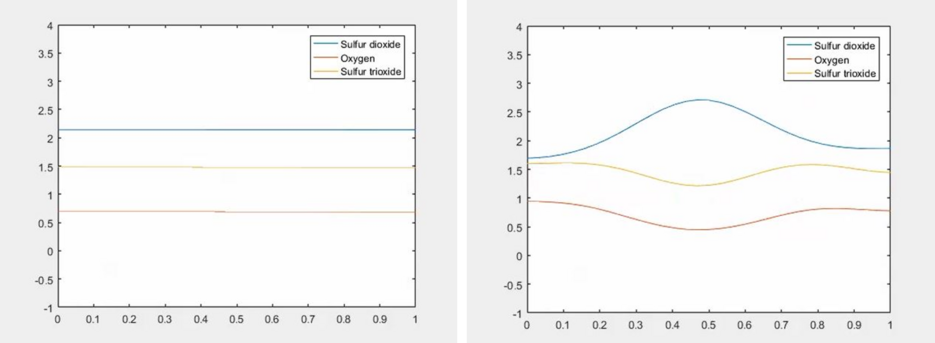
  • Existence and regularity of reaction-diffusion systems
  • Entropy method and convergence to equilibrium
  • Molecular communications
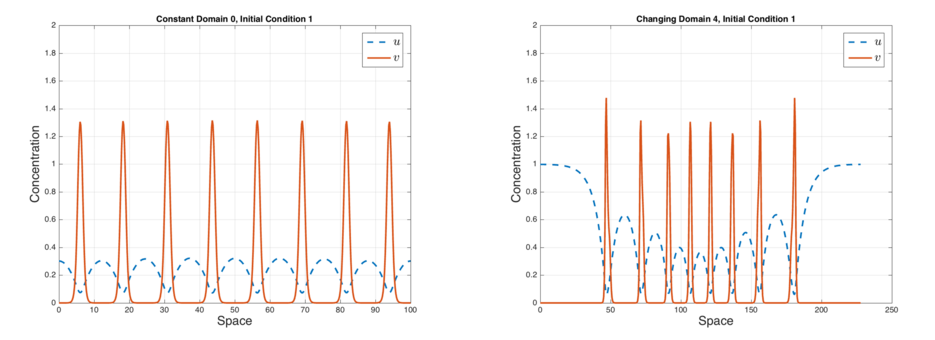
  • Pattern formation in evolving domains
  • Stabilisation by boundary noise for PDE
  • Energy equalities for equations from fluid mechanics
  • Attractors for deterministic/random dynamical systems from PDE

Our research is funded by

  • OeAD project CZ 03/2023 ''Reaction-Diffusion Systems with Non-local Diffusion'' (2023 - 2024)
  • OeAD project MULT 06/2023 "Mathematical investigation of hysteresis in material modeling" (2023 - 2025)
  • FWF Project I 5213 ”Quasi-steady state approximation for PDE”, 2022 - 2025
  • OeAD Project FR 03/2020 ”Toward rigorous designation of molecular communications systems”, 2021 - 2022.
Compley Systems and Dynamics: Plot
Compley Systems and Dynamics: Plot

Group Lead

Man with glasses in front of chalkboard.

Ass.-Prof. Dr.rer.nat. M.Sc.
Quoc Bao Tang

e-mail:
quoc.tang(at)uni-graz.at

Phone:+43 316 380 - 5175
Location:Heinrichstraße 36, 4. Stock, Raum 503
Opentimes:Nach Vereinbarung
Web: https://imsc.uni-graz.at/btang

Group secretariat

Scientific Staff

Nesibe Ayhan

e-mail:
nesibe.ayhan(at)uni-graz.at

Phone:+43 316 380 - 5068

Dr.
Bao-Ngoc Tran

e-mail:
bao-ngoc.tran(at)uni-graz.at

Phone:+43 316 380 - 5079
Web: https://sites.google.com/view/tranbaongoc-math/bio?authuser=0